The Playful Guide to Writing Pi in Python: Mastering Math with Code

Python, a versatile programming language, has become a tool of choice for many mathematicians and programmers. Among its numerous applications is the ability to calculate and represent mathematical constants, such as π (pi). In this playful guide, we’ll explore how to write pi in Python, delving into various methods and tricks to harness this iconic mathematical constant in your coding projects.

Understanding Pi and Its Significance in Python

Pi, denoted by the Greek letter π, is a fundamental mathematical constant representing the ratio of a circle’s circumference to its diameter. It is approximately equal to 3.14159, although its decimal representation goes on infinitely without repeating. The significance of pi transcends mere mathematical curiosity; it plays a pivotal role in various fields such as geometry, physics, and engineering. In the realm of computer programming, particularly in Python, comprehending pi’s importance is indispensable for performing precise calculations and simulations.

Pi in Circles and Spheres Calculations

In geometry, pi is instrumental in computing properties of circles and spheres. Here’s a breakdown of its significance in these contexts:

Application	Description
Circumference of a Circle	The formula for calculating the circumference (C) of a circle is given by C = 2πr, where ‘r’ denotes the radius of the circle. Pi is used here to relate the circumference to the circle’s radius.
Area of a Circle	The formula for calculating the area (A) of a circle is A = πr². Pi appears here to quantify the area enclosed by the circle.
Volume of a Sphere	In spheres, pi is employed in the formula for calculating volume (V), given by V = (4/3)πr³, where ‘r’ represents the radius of the sphere. Pi is crucial in determining the volume occupied by the sphere.

Python’s Utilization of Pi

Python, as a versatile programming language, leverages pi in various libraries and modules dedicated to advanced mathematical computations. Here are some key aspects of pi’s usage in Python:

• Math Module: Python’s math module provides access to mathematical functions, constants, and tools for numerical computations. It includes a constant math.pi, which holds the value of pi to a high degree of precision. Developers can utilize this constant in their programs for accurate mathematical calculations involving circles, spheres, trigonometry, and more;
• NumPy Library: NumPy, a fundamental package for numerical computing in Python, incorporates pi as numpy.pi. This constant is utilized extensively in array computations, scientific calculations, and data analysis tasks. Engineers, physicists, and researchers rely on NumPy’s efficient handling of mathematical operations, where pi plays a vital role;
• SciPy Library: SciPy, built upon NumPy, extends its capabilities to include advanced mathematical algorithms and functions for scientific computing. Pi finds applications in various scientific simulations, optimization problems, signal processing, and statistical analyses facilitated by SciPy’s extensive functionality;
• Sympy Library: Sympy, a Python library for symbolic mathematics, integrates pi as sympy.pi. Symbolic computation involving mathematical expressions, equations, and algebraic manipulations benefit from the accurate representation of pi provided by Sympy;
• Plotting Libraries: Python libraries such as Matplotlib and Plotly, commonly used for data visualization, often incorporate pi for creating plots of circular or periodic functions. Graphical representations of mathematical concepts heavily rely on pi for accurate depiction and analysis.

Basic Method: The math Module

Accessing the mathematical constant pi is straightforward, thanks to the built-in math module. This module offers precise mathematical functions and constants, including pi. Below are the steps to utilize pi from the math module:

Importing the math Module

Before using any functionality from the math module, it needs to be imported into the Python script or interactive session. This can be done using the import statement:

import math

Accessing Pi

Once the math module is imported, the constant pi can be accessed using the syntax math.pi. This grants access to the value of pi with a high degree of precision. For example:

import math
print(math.pi) # Outputs: 3.141592653589793

This example demonstrates how to import the math module and access the value of pi using the math.pi attribute. When executed, it prints out the value of pi with a precision of several decimal places.

Utilizing the math module provides not only a convenient way to access mathematical constants like pi but also ensures accuracy in mathematical computations. It’s particularly useful in scenarios where precise numerical results are required, such as scientific calculations, engineering applications, and mathematical modeling.

Advantages of Using the math Module

Aspect	Description
Precision	The math module offers a high degree of precision, ensuring accurate results in mathematical computations involving pi.
Ease of Use	Accessing pi through the math module is straightforward, requiring only a single import statement and referencing the math.pi attribute.
Versatility	In addition to pi, the math module provides a wide range of mathematical functions and constants, making it versatile for various mathematical tasks.
Standardization	Utilizing the math module adheres to Python’s standard library conventions, promoting code readability and maintainability.
Efficiency	The math module is optimized for performance, ensuring efficient execution of mathematical operations.

Generating Pi with a Series: Leibniz Formula

For those interested in computing pi in Python from scratch, the Leibniz formula provides a simple method. This formula represents pi as an infinite series.

The Leibniz Formula

The Leibniz formula for pi is:

Pi = 4/1 – 4/3 + 4/5 – 4/7 + 4/9 – …

This formula alternates between addition and subtraction, with each term becoming progressively smaller.

Python Implementation

Here’s how you can implement the Leibniz formula in Python:

def calculate_pi(terms):
pi = 0
for i in range(terms):
pi += ((-1) ** i) * (4 / (2 * i + 1))
return pi

Advantages of Using the Math Module for Pi Calculation

When working with pi in Python, leveraging the math module provides numerous advantages:

• Precision: The math module offers a high degree of precision, ensuring accurate results in mathematical computations involving pi;
• Ease of Use: Accessing pi through the math module is straightforward. It requires only a single import statement (import math) and referencing the math.pi attribute;
• Versatility: In addition to pi, the math module provides a wide range of mathematical functions and constants, making it versatile for various mathematical tasks;
• Standardization: Utilizing the math module adheres to Python’s standard library conventions, promoting code readability and maintainability;
• Efficiency: The math module is optimized for performance, ensuring efficient execution of mathematical operations.

Comparison with Leibniz Formula

While the Leibniz formula provides an interesting method for calculating pi, it may not be as efficient or precise as using the math module. Here’s a comparison:

Aspect	Leibniz Formula	Math Module
Precision	Moderate	High
Ease of Use	Requires custom implementation	Straightforward access via math.pi
Versatility	Limited to pi	Offers a wide range of mathematical functions and constants
Standardization	Custom implementation	Follows Python’s standard library conventions
Efficiency	May be slower for large numbers of terms	Optimized for performance

Using the numpy Library

For those engaged in scientific computing, utilizing numpy to compute pi in Python is a common practice. numpy is a powerful library that supports large, multi-dimensional arrays and matrices, making it well-suited for a wide range of numerical tasks.

Accessing Pi in numpy

You can easily access the value of pi in numpy using the following code:

import numpy as np
print(np.pi) # Outputs: 3.141592653589793

Advantages of Using numpy for Pi Calculation

When it comes to calculating pi in Python, numpy offers several advantages:

• Efficiency: numpy is optimized for numerical computations, making it efficient for calculations involving pi;
• Precision: numpy ensures high precision in mathematical computations, including those involving pi;
• Versatility: Beyond just providing the value of pi, numpy offers a wide range of mathematical functions and operations, enhancing versatility in numerical tasks;
• Ease of Use: Accessing pi in numpy is straightforward, requiring only a single import statement (import numpy as np) and referencing the np.pi attribute;
• Compatibility: numpy integrates seamlessly with other Python libraries commonly used in scientific computing, enabling smooth workflow integration.

Comparison with Other Methods

Let’s compare using numpy to access pi with previously discussed methods:

Aspect	numpy	Math Module	Leibniz Formula
Efficiency	Optimized for numerical computations	Optimized for performance	May be slower for large numbers of terms
Precision	High	High	Moderate
Versatility	Offers a wide range of mathematical functions and operations	Provides various mathematical functions and constants	Limited to pi
Ease of Use	Straightforward access via np.pi	Straightforward access via math.pi	Requires custom implementation
Compatibility	Integrates well with other Python libraries	Standard library in Python	Custom implementation

Visualizing Pi: Plotting a Circle in Python

Understanding how to calculate pi in Python can be further enhanced by visual representation, such as plotting a circle. This visual representation not only demonstrates a practical use of pi but also provides understanding of geometric principles. Here are the steps for plotting a circle:

• Import Libraries: Begin by importing the necessary libraries. In this case, we’ll use matplotlib.pyplot for plotting and math for mathematical operations, including accessing pi;
• Define Parameters: Define the parameters of the circle, such as its radius. Additionally, calculate the circumference of the circle using pi;
• Plot the Circle: Finally, plot the circle using matplotlib’s plotting functions.

Python Implementation

Here’s how you can implement the steps mentioned above:

import matplotlib.pyplot as plt
import math

# Define the circle's radius
radius = 1

# Calculate the circumference using pi
circumference = 2 * math.pi * radius

# Generate points to plot the circle
theta = [i * 0.01 for i in range(0, 628)] # Angle theta ranges from 0 to 2*pi
x = [radius * math.cos(t) for t in theta] # x-coordinate of points on the circle
y = [radius * math.sin(t) for t in theta] # y-coordinate of points on the circle

# Plot the circle
plt.figure(figsize=(6, 6))
plt.plot(x, y)
plt.axis('equal') # Ensure equal scaling of x and y axes
plt.title('Plot of a Circle')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show()

Educational Insights

By plotting a circle in Python, learners can deepen their understanding of pi and its relationship with geometry. This exercise not only reinforces the concept of pi as the ratio of a circle’s circumference to its diameter but also demonstrates how mathematical concepts can be visualized and explored using programming.

Pi in Monte Carlo Simulations

Monte Carlo simulations, renowned for their application in probabilistic modeling, also involve the utilization of pi. Python’s random module, combined with pi, enables the estimation of pi through simulation.

Monte Carlo Method to Estimate Pi

The Monte Carlo method for estimating pi involves the following steps:

• Generate Random Points: Randomly generate a large number of points within a square region;
• Determine the Ratio: Determine the ratio of points that fall inside a circle inscribed within the square to the total number of points generated;
• Calculate Pi: Use the obtained ratio to estimate the value of pi.

Python Example

Here’s an implementation of the Monte Carlo method in Python:

import random

def estimate_pi(num_points):
inside_circle = 0
for _ in range(num_points):
x, y = random.random(), random.random()
if x**2 + y**2 <= 1:
inside_circle += 1
return 4 * inside_circle / num_points

Educational Insights

Monte Carlo simulations offer a practical and intuitive way to estimate pi. By randomly sampling points within a square and calculating the ratio of points inside a circle, learners can grasp the concept of pi as the ratio of a circle’s area to the area of its circumscribing square. This hands-on approach not only reinforces the mathematical definition of pi but also illustrates the power of simulation techniques in solving complex problems.

Pi in Real-life Applications

Pi (π) is a mathematical constant representing the ratio of a circle’s circumference to its diameter. Its value is approximately 3.14159, though it continues infinitely without repeating. Let’s delve into some practical applications where pi is crucial and how it can be implemented in Python.

Engineering Applications

In engineering, pi finds extensive use, especially in calculating stresses in cylindrical structures such as pipes, pressure vessels, and beams. The formula for calculating stress in a cylindrical structure involves pi in determining cross-sectional areas and moments of inertia. Engineers utilize pi to accurately design and analyze various mechanical components.

Calculating the stress in a cylindrical pipe subjected to internal pressure involves pi in the formula:

​Astronomy Applications

Astronomy heavily relies on pi for calculating orbits, spherical volumes, and other celestial phenomena. When determining the trajectories of celestial bodies or calculating the volumes of planets and stars, astronomers utilize pi extensively. Additionally, pi plays a crucial role in understanding the geometry of celestial objects and their movements.

Calculating the volume of a spherical celestial body, such as a planet or star, involves pi in the formula:

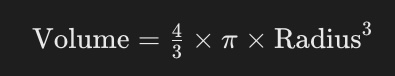
Implementing pi in Python

Python provides built-in support for mathematical operations, including pi. The math module in Python contains functions and constants related to mathematical calculations. To use pi in Python, one can import the math module and access the constant pi.

import math

# Accessing the value of pi
pi_value = math.pi
print("Value of pi:", pi_value)

By importing the math module and accessing the constant pi, you can incorporate the value of pi into your Python programs for various calculations.

Advanced Mathematical Concepts Using Pi

Python serves as a powerful tool for exploring advanced mathematical concepts, leveraging the mathematical constant π (pi). These concepts encompass a wide array of mathematical disciplines, including Fourier transformations, trigonometric functions, and calculus. Let’s delve into these topics and explore how Python facilitates their exploration.

Fourier Transformations

Fourier transformations are fundamental in various fields, particularly signal processing, image analysis, and physics. They decompose a complex waveform into its constituent sinusoidal components. π plays a pivotal role in Fourier transformations, particularly in defining the periodicity of functions and the frequency domain representation of signals.

Using Python, you can perform Fourier transformations on signals or functions using libraries such as NumPy and SciPy. By utilizing π, you can accurately represent periodic functions and analyze their frequency content.

import numpy as np
import matplotlib.pyplot as plt

# Generate a time vector
t = np.linspace(0, 2*np.pi, 1000)

# Create a sine wave
y = np.sin(t)

# Perform Fourier transformation
fourier_transform = np.fft.fft(y)

# Plot the results
plt.plot(np.abs(fourier_transform))
plt.xlabel('Frequency')
plt.ylabel('Magnitude')
plt.title('Fourier Transform')
plt.show()

Trigonometric Functions

Trigonometric functions such as sine and cosine are fundamental to mathematics and physics. These functions relate the angles of a right triangle to the lengths of its sides. π serves as a crucial parameter in defining the periodicity and amplitude of trigonometric functions.

Python allows you to calculate sine and cosine values using the math module, incorporating π in trigonometric calculations.

import math

# Calculate sine and cosine values using pi
angle = math.pi / 4 # π/4 radians
sin_value = math.sin(angle)
cos_value = math.cos(angle)

print("Sine:", sin_value)
print("Cosine:", cos_value)

Calculus

In calculus, π appears in integration and differentiation, particularly when dealing with circular or periodic functions. Integrals and derivatives involving π are common in various mathematical and scientific contexts, such as calculating areas under curves or rates of change.

Python enables the computation of integrals and derivatives involving π using libraries like SymPy or SciPy.

import sympy as sp

# Define a symbolic variable and function
x = sp.symbols('x')
f = sp.sin(x)

# Compute the integral involving pi
integral = sp.integrate(f, (x, 0, sp.pi))

# Compute the derivative involving pi
derivative = sp.diff(f, x)

print("Integral:", integral)
print("Derivative:", derivative)

Conclusion

Learning how to write pi in Python is more than a mathematical exercise; it’s a journey into the heart of coding and mathematics. Whether you’re a beginner dabbling in Python or an experienced programmer, understanding the various ways to incorporate pi into your Python code can open up a world of possibilities in both computational mathematics and practical applications. With Python’s simplicity and versatility, mastering how to write pi is both a fun and enlightening endeavor.

FAQ