Exponentially Fun: Mastering Exponents in Python

Exponents are a fundamental concept in mathematics and computing, representing the power to which a number is raised. In Python, handling exponents is a straightforward and essential skill, especially for those diving into data science, machine learning, or even basic arithmetic operations. This article guides you through various ways of how to do exponents in Python, along with practical examples and common scenarios where they are used. By the end of this article, you’ll be well-equipped to use Python for any exponential calculations.

Understanding Exponents in Python

Before delving into the practical side, let’s take a moment to grasp the concept of exponents. Exponents are a fundamental mathematical concept that represents repeated multiplication of a number by itself. In simple terms, an exponent tells us how many times a base number should be multiplied by itself. It is denoted by a superscript to the right and above the base number. For example, in the expression “a to the power of b”, “a” is the base and “b” is the exponent.

In Python programming, we often encounter situations where we need to raise a number to a certain power. This process, known as exponentiation, is facilitated by the power operator “**”. This operator efficiently performs exponentiation by raising the base number to the power of the exponent. Now, let’s delve into practical examples to solidify our understanding of exponents in Python.

Basic Exponentiation

The simplest form of exponentiation involves raising a base number to a positive integer exponent. Consider the following example:

base = 2
exponent = 3
result = base ** exponent
print("Result:", result) # Output: 8

In this example, “base” is raised to the power of “exponent”, resulting in 2 to the power of 3, which equals 8.

Exponentiation with Variables

Exponents can involve variables as well. Let’s see how we can use variables in exponentiation:

x = 3
y = 2
result = x ** y # x raised to the power of y
print("Result:", result) # Output: 9

Here, we raise the value of variable “x” to the power of variable “y”, resulting in 3 to the power of 2, which equals 9.

Negative Exponents

Negative exponents represent the reciprocal of the base raised to the positive exponent. Let’s explore how to handle negative exponents in Python:

python
Copy code
result = 2 ** -2 # Equivalent to 1 / (2 ** 2)
print("Result:", resul

In this example, 2 is raised to the power of -2, which is equivalent to 1 divided by 2 to the power of 2, resulting in 0.25.

Fractional Exponents

Fractional exponents denote taking the root of a number. While Python’s power operator handles integer exponents seamlessly, fractional exponents require the “math.pow()” function from the “math” module:

import math
result = math.pow(4, 0.5) # Square root of 4
print("Result:", result) # Output: 2.0

Here, we use “math.pow()” to calculate the square root of 4, resulting in 2.0.

The Power Operator **

One of the primary tools at our disposal for dealing with exponents is the ** operator. This operator, while seemingly simple, holds significant power in Python’s arsenal. Let’s embark on a journey to delve deeper into its nuances, exploring its syntax, functionality, advantages, and practical applications.

Understanding the Syntax of the Power Operator

At its core, the syntax of the ** operator is elegantly simple:

result = base ** exponent

Here, base denotes the number to be raised to a power, while exponent represents the power to which the base is raised.

A Practical Example

Let’s illustrate the usage of the ** operator with a concrete example:

# Raising a number to a power in Python
base = 2
exponent = 3
result = base ** exponent
print(result) # Output: 8

In this example, we assign the value 2 to base and 3 to exponent, and then compute the result using the ** operator. The output, as expected, is 8, demonstrating the fundamental concept of exponentiation.

Deeper Dive: Exploring the Code Snippet

Breaking down the aforementioned code snippet:

• base = 2: We initialize the variable base with the value 2, which serves as the base number for exponentiation;
• exponent = 3: The variable exponent is set to 3, indicating the power to which the base will be raised;
• result = base ** exponent: Using the ** operator, we calculate the result by raising base to the power of the exponent;
• print(result): Finally, we print the result of the exponentiation operation, which is 8 in this case.

Advantages of the ** Operator

Employing the ** operator for exponentiation in Python offers numerous advantages:

• Simplicity: The syntax is concise and intuitive, facilitating easy comprehension and utilization;
• Efficiency: Python’s ** operator is highly efficient, ensuring swift execution times for exponentiation tasks;
• Versatility: It supports both integer and floating-point exponentiation, catering to a wide range of use cases.

Handling Larger Exponents

One of the notable strengths of the ** operator is its ability to handle not only small integer exponents but also larger or even floating-point values. Consider the following example:

base = 10
exponent = 0.5
result = base ** exponent
print(result) # Output: 3.1622776601683795

In this instance, we compute the square root of 10 using the ** operator, yielding approximately 3.162 as the result.

Using the pow() Function

In addition to the ** operator, Python provides another powerful tool for handling exponential calculations: the built-in pow() function. This function offers versatility and flexibility, making it ideal for scenarios involving large numbers or modular exponentiation. Let’s delve into the syntax, functionality, and practical applications of the pow() function in Python programming.

Syntax of the pow() Function

The pow() function in Python has a straightforward syntax:

result = pow(base, exponent, modulus)

Here, base represents the base number, exponent denotes the power to which the base is raised, and modulus (optional) specifies the modulus for modular exponentiation.

Example Usage

Let’s illustrate the application of the pow() function with a simple example:

# Using the pow() function
result = pow(2, 3)
print(result) # Output: 8

In this example, we utilize the pow() function to compute 2 raised to the power of 3. The resulting output is 8, demonstrating the functionality of the pow() function in performing exponential calculations.

Exploring the Code Snippet

Breaking down the code snippet:

• result = pow(2, 3): We invoke the pow() function with arguments 2 and 3, representing the base and exponent, respectively. The function calculates 2 raised to the power of 3 and assigns the result to the variable result;
• print(result): Finally, we print the result of the exponential calculation, which is 8 in this case.

Advantages of the pow() Function

The pow() function offers several advantages for handling exponential calculations in Python:

• Flexibility: It supports both integer and floating-point exponents, providing flexibility in various mathematical scenarios;
• Modular Exponentiation: The pow() function can be used for modular exponentiation by specifying the modulus parameter, enabling efficient handling of cryptographic and number theory applications;
• Handling Large Numbers: In scenarios involving large numbers, pow() can efficiently compute exponentiation, avoiding potential overflow errors.

Modular Exponentiation with pow()

The pow() function excels in modular exponentiation, a crucial operation in cryptography and number theory. Consider the following example:

base = 2
exponent = 3
modulus = 5
result = pow(base, exponent, modulus)
print(result) # Output: 3

In this example, we compute
23
2
3
modulo 5 using the pow() function, resulting in 3 as the output.

Utilizing Math and Numpy Libraries

Python’s built-in math and NumPy libraries provide robust solutions for such scenarios, offering enhanced performance and versatility. Let’s explore how these libraries can be leveraged for exponential calculations and delve into practical examples showcasing their capabilities.

Using the math Library

Python’s math library provides a comprehensive set of mathematical functions, including the pow() function for exponentiation. Let’s see how it can be used:

import math

# Using the math library
result = math.pow(2, 3)
print(result) # Output: 8.0

In this example, we utilize the math.pow() function to compute
23
2
3
. The result, 8.0, is a floating-point number, demonstrating the ability of the math library to handle exponentiation with precision.

Leveraging NumPy for Array Operations

While the math library is suitable for scalar operations, NumPy excels in array-based computations, offering enhanced performance and convenience. Let’s explore how NumPy’s power function can be used for array operations:

import numpy as np

# Using NumPy for array operations
arr = np.array([2, 3, 4])
exponents = np.array([3, 2, 1])
results = np.power(arr, exponents)
print(results) # Output: [8, 9, 4]

In this example, we create NumPy arrays arr and exponents, representing the base numbers and corresponding exponents, respectively. By applying NumPy’s power function np.power(), we efficiently compute the element-wise exponentiation of the arrays, yielding the results [8, 9, 4].

Advantages of Using Math and NumPy Libraries

Criteria	Description
Efficiency	NumPy’s array-based operations are highly optimized, offering superior performance, especially for large datasets.
Versatility	Both math and NumPy libraries support various data types, enabling seamless handling of integer and floating-point exponentiation.
Convenience	NumPy’s array operations allow for concise and expressive code, facilitating complex computations with minimal effort.

Practical Applications of Exponents in Python

Now that we know how to do exponents in Python, let’s explore some practical applications. Exponents are widely used in fields like finance for compound interest calculations, in physics for exponential decay models, and in computer science for algorithms and data processing.

Compound Interest Calculation

One of the most common applications of exponents is in finance, particularly in compound interest calculations. Compound interest refers to the interest calculated on the initial principal and also on the accumulated interest from previous periods. This compounding effect can be modeled using exponential functions.

The formula for compound interest is given as:

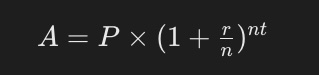
Where:

• A is the amount of money accumulated after t years, including interest;
• P is the principal amount (initial investment);
• r is the annual interest rate (in decimal);
• n is the number of times interest is compounded per time period;
• t is the time in years.

Let’s implement this formula in Python:

# Compound interest formula: A = P * (1 + r/n)^(nt)
P = 1000 # Principal amount
r = 0.05 # Annual interest rate
n = 12 # Number of times interest applied per time period
t = 5 # Time in years

A = P * (1 + r/n) ** (n * t)
print(A)

In this example, we calculate the amount of money accumulated after 5 years with a principal amount of $1000, an annual interest rate of 5%, compounded monthly.

Exponential Growth

Exponential growth models are prevalent in various scientific disciplines, such as physics, biology, and economics. These models describe phenomena where a quantity increases or decreases at a rate proportional to its current value. Exponential growth is characterized by rapid increases over time, governed by an exponential function.

The formula for exponential growth is represented as:

Where:

• y is the final amount after growth;
• a is the initial amount;
• b is the growth rate per unit of time;
• x is the time.

Let’s implement an exponential growth calculation in Python:

# Exponential growth formula: y = a * b^x
a = 2 # Initial amount
b = 1.1 # Growth rate
x = 5 # Time

y = a * b ** x
print(y)

In this example, we compute the final amount after 5 units of time with an initial amount of 2 and a growth rate of 10%.

Conclusion

Mastering how to do exponents in Python is an essential skill for anyone interested in programming, data analysis, or scientific computing. This article has walked you through various methods of handling exponents in Python, from basic operations to advanced scenarios involving libraries like numpy. Understanding these concepts will not only enhance your coding skills but also open up a world of possibilities for mathematical and scientific exploration in Python.

Exponents, a seemingly simple concept, are incredibly powerful in programming, offering solutions to complex problems across various domains. By learning how to do exponents in Python, you’re equipping yourself with a vital tool in your programming arsenal. Whether you’re a beginner or an experienced coder, this knowledge is invaluable for your journey in Python programming.

FAQ